Traversing Algorithm

The algorithm for analyzing the graph is shown in the BridgeWalk class in Listing 2. The __init__ constructor from line 3 defines three instance variables: graph for storing the graph structure from Listing 1, a dictionary named bridges that gets populated by the for loop as of line 8 with keys from all bridges defined in the graph, and maxpath, a list with the longest path found over the seven bridges during the run. Listing 1 calls the explore() method without parameters as of line 21; the corresponding definition in Listing 2 only shows the self placeholder as a parameter, which is common in Python classes, for the code to make object-specific calls with it later.

The for loop from line 15 in Listing 2 iterates through all node definitions in the graph and calls the scan() method with the number of the current node as a starting point. Since scan() is also called recursively later when two more parameters are passed to it – the current path as a list and a dictionary with the bridges encountered so far (seen) – the function definition in line 18 predefines them as the empty list and the empty dictionary if they are missing, which is the case on the first call.

The two for loops in lines 20 and 22 try all possibilities for moving from the current node to the next one and cover all directly connected nodes as well as any bridges to connect them. To see whether a bridge is walkable (i.e., make sure it has not been accessed before), the bridge_ok method checks whether it already exists in the seen dictionary; if it cannot find the bridge there, it picks it and marks the traversal in line 29 by setting the key in seen to a value of 1.

It also appends the bridge name to the path in path. If the path is longer than the longest in maxpath so far, line 33 stores a copy there so that the program can retrieve the longest path data later.

Isolating

When the algorithm enters a new bridge, the path continues from there, using recursion, by line 36 again calling the scan() method, going back to line 18, but now passing the new target node from the fork as a parameter. The values for path and seen, passed to bridge_ok() in line 24, provide the function with information but are also modified by it. You need to pay attention here: Parts of the code leading up to this point (the for loops in lines 20 and 22) require the unmodified data structures, because they want to pick fresh, not already trodden, paths.

The solution to the dilemma lies in encapsulating the check in bridge_ok() together with the .copy() calls in line 24, which do not pass the two parameters as pointers, as is usual in Python, but as separate copies. When all possibilities are exhausted, at the end of the run, Listing 1 prints the message

['a', 'b', 'f', 'g', 'd', 'e']
Impossible!

because it could only connect six bridges. Leonhard Euler was, of course, right.

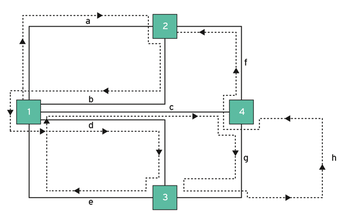
Now, if Kaliningrad were to build another bridge, h, connecting nodes 3 and 4 parallel to bridge g (see Figure 3), the city could offer a repetition-free tour! To prove that, we modify the graph definition in Listing 1 according to Listing 3 and run the script again:

$ ./solved.py
['a', 'b', 'd', 'e', 'c', 'g', 'h', 'f']
Solved!

Figure 3: The path h reduces the number of odd nodes to two and paves the way to a solution.

01 "3" : [["1", ["d", "e"]],
02        ["4", ["g","h"]],
03       ],
04 "4" : [["2", ["f"]],
05        ["3", ["g","h"]],
06        ["1", ["c"]]
07       ]

Figure 3 shows that an odd number of bridges is attached to only two of the four nodes, thus fulfilling Euler's requirement. The corresponding change in the data structure shown in Listing 3 builds a bridge h between nodes 3 and 4 and, as the output above shows, solves the problem with the same algorithm – something for the Kaliningrad city fathers to consider, for sure.