Geometric construction of self-similar patterns
Fun with Fractals
Article from Issue 147/2013
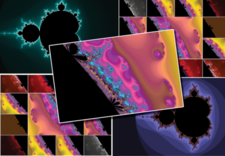
Gnofract 4D is a different kind of graphics program that conjures up stunning graphics videos based on fractal mathematics.
Self-similarity is found in mathematics, nature, and systems, such as stock markets, network traffic, and stress fractures.
The whole of a self-similar object is similar to a part of its internal structures. Imagine, for example, our earth, which is known to be more or less round. If you were to descend to the surface from a satellite view and see that the continents, mountains, cities, and houses were all spheres, the earth would be reflected in smaller, self-similar objects. Of course, this is not the case, so you need to consider other objects on our home planet.
Buy this article as PDF
Express-Checkout as PDF
Price $2.95
(incl. VAT)
(incl. VAT)
Buy Linux Magazine
TABLET & SMARTPHONE APPS
US / Canada
UK / Australia