Looking for an edge with the classic Quicksort algorithm
Peaceful Combination
Admittedly, both implementation strategies for Quicksort have their advantages and disadvantages. The imperative strategy in Listing 1 requires no additional memory but almost completely obscures the elegant structure of the algorithm. The functional strategy in Listing 2 and Listing 3 looks very elegant but creates a new list with each recursion. Is it possible to combine the advantages of both worlds?
Yes, it is. The following implementation in C++ is based on std::partition [4], an algorithm from the Standard Template Library that partitions a range based on an element. std::partition in Listing 4 does the job of list comprehension in Listing 2 and Listing 3.
Listing 4
Quicksort in C++
template <typename Forward>;
void quicksort(ForwardIt first, ForwardIt last) {
if(first == last) return;
auto pivot = *std::next(first, std::distance(first,last)/2);
ForwardIt middle1 = std::partition(first, last, [pivot](const auto& em){return em < pivot;});
ForwardIt middle2 = std::partition(middle1, last, [pivot](const auto& em){return !(pivot < em);});
quicksort(first, middle1);
quicksort(middle2, last);
}
The Crucial Question
But this article has not yet answered the crucial question in C++: "Say, how fast are you?"
In C++17, C++ introduced support for the Parallel Standard Template Library (STL). Around 70 of the more than 100 algorithms in the STL can be executed sequentially, executed in parallel, or vectorized by means of a policy. However, so far only the Microsoft compiler supports parallel execution of the STL algorithms, which is why the following performance values are based on the MS compiler. All performance figures are taken from a program compiled for maximum optimization and executed with eight cores. Listing 5 uses a slightly modified variant of the Quicksort algorithm from Listing 4.
Listing 5
Performance Test
01 #include <algorithm>
02 #include <chrono>
03 #include <execution>
04 #include <iomanip>
05 #include <iostream>
06 #include <iterator>
07 #include <numeric>
08 #include <random>
09 #include <vector>
10
11 template <typename ExecutionPolicy, typename ForwardIt>
12 void quicksort(ExecutionPolicy&& policy, ForwardIt first, ForwardIt last) {
13 if(first == last) return;
14 auto pivot = *std::next(first, std::distance(first,last)/2);
15 ForwardIt middle1 = std::partition(policy, first, last, [pivot](const auto& em){ return em < pivot; });
16 ForwardIt middle2 = std::partition(policy, middle1, last, [pivot](const auto& em){ return !(pivot < em); });
17 quicksort(policy, first, middle1);
18 quicksort(policy, middle2, last);
19 }
20
21 std::vector<int> getRandomVector(int numberRandom, int lastNumber) {
22 std::random_device seed;
23 std::mt19937 engine(seed());
24 std::uniform_int_distribution<int> dist(0, lastNumber);
25 std::vector<int> randNumbers;
26 randNumbers.reserve(numberRandom);
27 for
28 (int i=0; i < numberRandom; ++i){
29 randNumbers.push_back(dist(engine));
30 }
31 return randNumbers;
32 }
33
34 int main() {
35
36 std::cout << :*\n:*;
37
38 constexpr int numberRandom = 100:*000:*000;
39 constexpr int lastNumber = 100;
40
41 std::vector randVec = getRandomVector(numberRandom, lastNumber);
42
43 std::cout << numberRandom << " random numbers between 0 and " << lastNumber << "\n\n";
44
45 {
46 std::vector tmpVec = randVec;
47 std::cout << std::fixed << std::setprecision(10);
48 auto begin = std::chrono::steady_clock::now();
49 quicksort(std::execution::seq, tmpVec.begin(), tmpVec.end());
50 std::chrono::duration<double> last= std::chrono::steady_clock::now() - begin;
51 std::cout << "Quicksort sequential: " << last.count() << :*\n:*;
52 }
53
54 {
55 std::vector tmpVec = randVec;
56 std::cout << std::fixed << std::setprecision(10);
57 auto begin = std::chrono::steady_clock::now();
58 quicksort(std::execution::par, tmpVec.begin(), tmpVec.end());
59 std::chrono::duration<double> last= std::chrono::steady_clock::now() - begin;
60 std::cout << "Quicksort parallel: " << last.count() << :*\n:*;
61 }
62
63 std::cout << "\n\n";
64
65 {
66 std::vector tmpVec = randVec;
67 std::cout << std::fixed << std::setprecision(10);
68 auto begin = std::chrono::steady_clock::now();
69 std::sort(std::execution::seq, tmpVec.begin(), tmpVec.end());
70 std::chrono::duration<double> last= std::chrono::steady_clock::now() - begin;
71 std::cout << "std::sort sequential: " << last.count() << :*\n:*;
72 }
73
74 {
75 std::vector tmpVec = randVec;
76 std::cout << std::fixed << std::setprecision(10);
77 auto begin = std::chrono::steady_clock::now();
78 std::sort(std::execution::par, tmpVec.begin(), tmpVec.end());
79 std::chrono::duration<double> last= std::chrono::steady_clock::now() - begin;
80 std::cout << "std::sort parallel: " << last.count() << :*\n:*;
81 }
82
83 std::cout << :*\n:*;
84 }
The algorithm in Listing 5 includes an execution strategy (Line 12). This lets you control whether the algorithm is called sequentially (std::execution::seq in Lines 49 and 69) or in parallel (std::execution::par in Lines 58 and 78). Put simply, the program sorts a vector of 100,000,000 random elements (Line 38) between 0 and 100 (Line 39) and measures the performance four times.
The task of generating the equally distributed random numbers is handled by the getRandom function in Line 21. The vector is sorted both sequentially (Lines 45 to 52) and in parallel (Lines 54 to 61) with the quicksort function and sequentially (Lines 65 to 72) and in parallel (lines 74 to 81) with std::sort from the STL. In doing so, std::sort applies a hybrid method under the hood that also uses Quicksort. If you are interested in the details of Microsoft's implementation of std::sort, you can check them out on GitHub [5].
In addition to the execution strategy, two other C++17 features are used in this example. On the one hand, numbers can be represented in a readable way (100'000'000) with ticks; on the other, the compiler can automatically determine the type of a class template: std::vector tmpVec = randVec instead of std::vector<int> tmpVec = randVec.
Size Matters
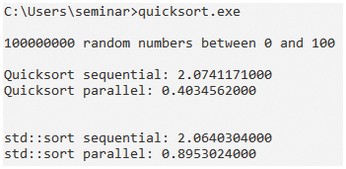
But now back to the crucial question. Given 100,000,000 random numbers in the range of 0 to 100, the Quicksort executed in parallel is impressively fast (Figure 3). It beats the sequential variant by a factor of 5 and is more than twice as fast as the std::sort executed in parallel. However, this relation changes significantly if the range from which the random numbers are taken in a uniform distribution grows significantly.
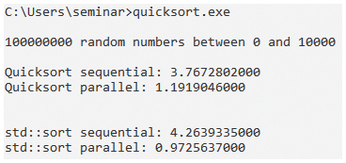
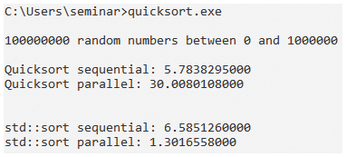
Regardless of whether the range increases to 0 to 10,000 (Figure 4) or 0 to 1,000,000 (Figure 5), the std::sort executed in parallel beats the sequentially-executed version by a factor of about 4. But the superior performance of parallel execution dwindles significantly as the range increases. For random numbers between 0 and 1,000,000, parallel execution is slower than sequential execution by a factor of 5.
What can these serious differences in performance be attributed to? We will not be analyzing the problem exhaustively, but only looking to provide some food for thought.
The main difference between 100,000,000 random numbers between 0 and 100 and between 0 and 1,000,000 is that, in the first case, on average, 1,000,000 equal numbers (1,000,000/100) and in the second case, on average, 100 equal numbers (100,000,000 / 1,000,000) end up in the random vector. In particular, this means that the call to std::partition [4] is far more efficient in the first case, since it has to swap significantly fewer elements relative to the pivot element. Moreover, this write access requires synchronization between threads.
Now I have to get personal. During my long time as a C++ software developer and now as a C++ trainer, I have become prejudiced: "Don't think you can beat the performance of STL algorithms in general." I almost gave up on my fixed opinion after the first run with the random numbers between 0 and 100; however, the further performance tests just reinforced it.
« Previous 1 2 3 Next »
Buy this article as PDF
(incl. VAT)
