Geometric construction of self-similar patterns

Fun with Fractals

Article from Issue 147/2013
Author(s):

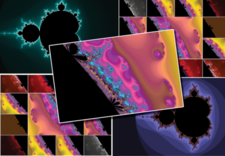
Gnofract 4D is a different kind of graphics program that conjures up stunning graphics videos based on fractal mathematics.

Self-similarity is found in mathematics, nature, and systems, such as stock markets, network traffic, and stress fractures.

The whole of a self-similar object is similar to a part of its internal structures. Imagine, for example, our earth, which is known to be more or less round. If you were to descend to the surface from a satellite view and see that the continents, mountains, cities, and houses were all spheres, the earth would be reflected in smaller, self-similar objects. Of course, this is not the case, so you need to consider other objects on our home planet.

Buy this article as PDF

Express-Checkout as PDF
Price $2.95
(incl. VAT)

Buy Linux Magazine

SINGLE ISSUES
Print Issues
Digital Issues
 
SUBSCRIPTIONS
Print Subs
Digisubs
 
TABLET & SMARTPHONE APPS
Get it on Google Play

US / Canada

Get it on Google Play

UK / Australia

Related content

  • Flam3 and Fractal Fr0st

    Few fractal algorithms create as beautiful and ethereal structures as Flam3. The Fr0st GUI helps you master the complex software.

    more »
  • First KDE 4.2 Beta Emerges as Caterpillar

    KDE 4.2 Beta1 (a.k.a. "Caterpillar") provides a new user experience: messaging, wallpaper via plug-ins, and Vi input mode for KWrite and Kate.

    more »
  • Julia

    Parallel processing is indispensable today – particularly in the field of natural sciences and engineering. Normal desktop users, however, can also benefit from higher performance through parallel execution with at least four calculation cores.

    more »
  • MEETING THE PANEL
    more »
  • KDE 4.3

    At the beginning of August, the KDE project released the third major update of KDE 4 – reason enough to put KDE 4.3 through its paces and study the new features.

    more »
comments powered by Disqus

Visit Our Shop

Trial Subscription

Digital Subscription

Subscribe

Direct Download

Read full article as PDF:

Price $2.95

News

Tag Cloud

Administration Community Events Hardware Linux Linux New Media Linux Pro Magazine Mobile Programming Software Ubuntu Web Development Windows free software open source