Illustrating mathematical concepts in video with Manim
Explainer

Manim lets you program video sequences with a few lines of Python code to present mathematical problems in an engaging and scientifically accurate way.
A precise description of a complex problem is sometimes difficult to achieve. Plain text will work eventually, but it often requires a great deal of imagination on the part of the reader. In a conventional classroom setting, an instructor might attempt to illustrate a topic by drawing on a chalkboard or whiteboard during a lecture, but it is fair to ask whether the power of the computer might offer a better option than a professor talking and writing at the same time. Presentation tools such as Impress or PowerPoint evolved as a way to illustrate key concepts in advance, but these tools typically have limited support for mathematical expressions, and they tend to present information in a static, slide show format. Movies and video sequences, on the other hand, can follow a spoken presentation organically in a way that often enhances learning and builds understanding.
However, shooting, trimming, and post-editing video footage can take time, even if you are experienced with video production. Manim [1] is a computer graphics tool that speeds up the task of building mathematical relationships into videos (Figure 1), letting you create a graphic video image with a simple Python script.
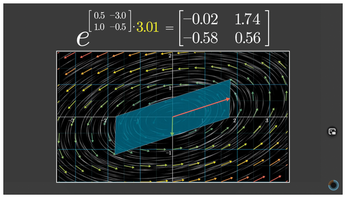
[...]
Buy this article as PDF
(incl. VAT)
Buy Linux Magazine
Subscribe to our Linux Newsletters
Find Linux and Open Source Jobs
Subscribe to our ADMIN Newsletters
Support Our Work
Linux Magazine content is made possible with support from readers like you. Please consider contributing when you’ve found an article to be beneficial.

News
-
Linux Kernel Project Releases Project Continuity Document
What happens to Linux when there's no Linus? It's a question many of us have asked over the years, and it seems it's also on the minds of the Linux kernel project.
-
Mecha Systems Introduces Linux Handheld
Mecha Systems has revealed its Mecha Comet, a new handheld computer powered by – you guessed it – Linux.
-
MX Linux 25.1 Features Dual Init System ISO
The latest release of MX Linux caters to lovers of two different init systems and even offers instructions on how to transition.
-
Photoshop on Linux?
A developer has patched Wine so that it'll run specific versions of Photoshop that depend on Adobe Creative Cloud.
-
Linux Mint 22.3 Now Available with New Tools
Linux Mint 22.3 has been released with a pair of new tools for system admins and some pretty cool new features.
-
New Linux Malware Targets Cloud-Based Linux Installations
VoidLink, a new Linux malware, should be of real concern because of its stealth and customization.
-
Say Goodbye to Middle-Mouse Paste
Both Gnome and Firefox have proposed getting rid of a long-time favorite Linux feature.
-
Manjaro 26.0 Primary Desktop Environments Default to Wayland
If you want to stick with X.Org, you'll be limited to the desktop environments you can choose.
-
Mozilla Plans to AI-ify Firefox
With a new CEO in control, Mozilla is doubling down on a strategy of trust, all the while leaning into AI.
-
Gnome Says No to AI-Generated Extensions
If you're a developer wanting to create a new Gnome extension, you'd best set aside that AI code generator, because the extension team will have none of that.

