An introduction to quantum computing
Compute Steps
Quantum algorithms are often represented as quantum circuits, as shown in Figure 2. A gate designated as H is applied to a bit in the output state |0>. Finally, a measurement is made. H is known as a Hadamard transform; it converts:
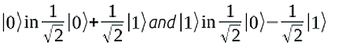
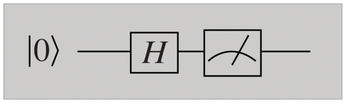
This algorithm works as follows: The qubit state is initially |0>, which the H gate changes to:
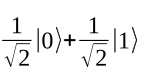
The final measurement destroys the superposition, as described above. You see |1> or |0> with a probability of 1/2 in each case. This approach has important applications. For example, classical calculators achieve only pseudo-random results, but the circuit shown in Figure 2 produces genuinely random values.
A detailed overview of quantum algorithms is provided by the Quantum Algorithm Zoo website [2]. The computational steps available for quantum bits are always transformations like H. They need to comply with certain characteristics: Among other things, they are always reversible, representable as matrices, and therefore linear. Mathematically speaking, these are unitary transformations. Another example is the bit flip X, also known as the Pauli-X gate. X maps |0> to |1> and vice versa. In general, a|0> + b|1> changes to the state b|1> by applying X to the state b|0> + a|1>.
Multiple Bits
You can program a random generator with one qubit, but for meaningful calculations, you need as many of them as possible. If you find the following calculations too detailed and time-consuming, just skip them for now. But if you want to program the circuits shown yourself on a quantum computing platform, the explanations will help you understand what actually happens.
In Figure 3, you can see a circuit with two qubits. The first is initialized with |0> and is in the following state after applying H:
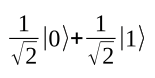
The second qubit is in the following state after applying H to |1>:
If you consider both qubits as one register, then you can multiply the superpositions by each other:
On the left of the equation is a description of the first qubit, and on the right a description of the second. Fortunately, you can multiply in the usual way, starting with:
This results is 1/2|0>|0> or written another way 1/2|00>; all told, the result is 1/2|00> – 1/2|01> + 1/2|10> – 1/2|11>.
|01> here means that the first qubit has a value of |0> and the second has a value of |1>. In other words, you are looking at a superposition for the four possible assignments of two legacy bits. Similarly, for three qubits, the result is a superposition of eight classical assignments; in general, n qubits give you a superposition for 2n.
I have now described how transformations are applied to the individual bits in a circuit. If I add gates that act on several bits, I can implement all quantum algorithms in this manner.
Computers specializing in quantum annealing [3], such as those marketed by the Canada's D-Wave Systems, differ from this approach. They use heuristics for optimization problems that can be viewed as a quantum version of classical simulated annealing [4]. Quantum computing can offer huge speed gains for certain inputs, but not for others.
Entanglement
There is a fascinating phenomenon that Einstein once referred to as "spooky action at a distance." Consider the following superposition:
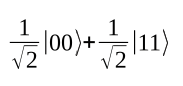
There is a quantum register of two bits. The amplitudes of the bit assignments |00> and |11> are each the reciprocal of the square root of 2, the amplitudes of |01> and |10> are each 0. This is known as a Bell state.
Now measure the register: With a probability of 1/2, both bits have a value of |1>, and both have a value of |0> with the same probability. Now separate the two bits by sending bit 2 to a colleague at a different location. Photon-based qubits can be transported over a fiber optic line, for example. Now measure bit 1, which you kept. There is a probability of 1/2 of seeing |1>, and the same probability of seeing |0>. Then call a colleague at the end of the fiber optic line and ask them to measure the other qubit. What will they see? In any case, it will be the same bit value measured for bit 1.
If your colleague measures their qubit first and you then measure yours, you will see the same amazing result: Before a measurement, both bits of the Bell state are undetermined; randomness determines the value after the measurement. But once you have measured one of the bits, the result of a future measurement on the other bit is immediately defined; in this case, it can be at a location an arbitrary distance away.
The qubits are entangled in the Bell state. Quantum teleportation uses this amazing behavior: In this process, a quantum bit is transmitted without having to traverse space itself. Instead, as above, you transport one qubit of a Bell pair to the target in advance. But information transfer does not take place at a speed faster than light.
Although this scenario sounds like science fiction, it has some very real applications. Quantum repeaters for building quantum communication networks face two challenges. On the one hand, qubits are changed during the measurement, and on the other hand, they cannot be copied – this is what no-cloning states. But how do you know a qubit can't be copied? We already know that operations on quantum bits must have a special mathematical property, which is referred to as being "unitary." This is because quantum physical systems evolve exclusively in a unitary manner, at least until a measurement is made. Now it can be shown that there is no transformation capable of copying an arbitrary quantum state to another. On the other hand, the two challenges for a repeater mentioned above can be used for cryptography. A sniffer cannot copy a qubit that is transferred, and encryption protocols can detect the modification caused by measuring.
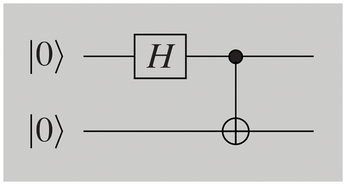
You can generate the Bell state with the circuit in Figure 4. Two bits are initialized with |0>; the gate H is applied to the first one. This is followed by a new operation, the two-bit CNOT (controlled-NOT or also controlled-X) transformation. This gate flips the second bit if, and only if, the first gate has a value of 1. In other words, |00> is converted to |00>, |01> to |01>, |10> into |11>, and |11> to |10>, in parallel for each component of a superposition.
In other words, the circuit performs the following calculation: |00> is changed by H to
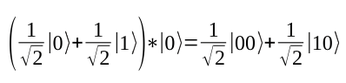
CNOTting results in the following:
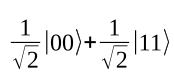
More than two qubits can also be entangled. This means that the circuit in Figure 5 can be used to generate the GHZ state (named after Greenberger, Horne, and Zeilinger):
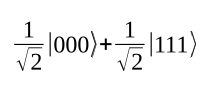
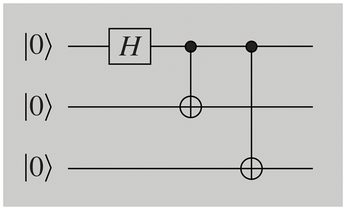
Measuring one of the three bits determines the state of the other two.
« Previous 1 2 3 Next »
Buy this article as PDF
(incl. VAT)
Buy Linux Magazine
Subscribe to our Linux Newsletters
Find Linux and Open Source Jobs
Subscribe to our ADMIN Newsletters
Support Our Work
Linux Magazine content is made possible with support from readers like you. Please consider contributing when you’ve found an article to be beneficial.

News
-
Mozilla Plans to AI-ify Firefox
With a new CEO in control, Mozilla is doubling down on a strategy of trust, all the while leaning into AI.
-
Gnome Says No to AI-Generated Extensions
If you're a developer wanting to create a new Gnome extension, you'd best set aside that AI code generator, because the extension team will have none of that.
-
Parrot OS Switches to KDE Plasma Desktop
Yet another distro is making the move to the KDE Plasma desktop.
-
TUXEDO Announces Gemini 17
TUXEDO Computers has released the fourth generation of its Gemini laptop with plenty of updates.
-
Two New Distros Adopt Enlightenment
MX Moksha and AV Linux 25 join ranks with Bodhi Linux and embrace the Enlightenment desktop.
-
Solus Linux 4.8 Removes Python 2
Solus Linux 4.8 has been released with the latest Linux kernel, updated desktops, and a key removal.
-
Zorin OS 18 Hits over a Million Downloads
If you doubt Linux isn't gaining popularity, you only have to look at Zorin OS's download numbers.
-
TUXEDO Computers Scraps Snapdragon X1E-Based Laptop
Due to issues with a Snapdragon CPU, TUXEDO Computers has cancelled its plans to release a laptop based on this elite hardware.
-
Debian Unleashes Debian Libre Live
Debian Libre Live keeps your machine free of proprietary software.
-
Valve Announces Pending Release of Steam Machine
Shout it to the heavens: Steam Machine, powered by Linux, is set to arrive in 2026.

