Illustrating mathematical concepts in video with Manim
Explainer

Manim lets you program video sequences with a few lines of Python code to present mathematical problems in an engaging and scientifically accurate way.
A precise description of a complex problem is sometimes difficult to achieve. Plain text will work eventually, but it often requires a great deal of imagination on the part of the reader. In a conventional classroom setting, an instructor might attempt to illustrate a topic by drawing on a chalkboard or whiteboard during a lecture, but it is fair to ask whether the power of the computer might offer a better option than a professor talking and writing at the same time. Presentation tools such as Impress or PowerPoint evolved as a way to illustrate key concepts in advance, but these tools typically have limited support for mathematical expressions, and they tend to present information in a static, slide show format. Movies and video sequences, on the other hand, can follow a spoken presentation organically in a way that often enhances learning and builds understanding.
However, shooting, trimming, and post-editing video footage can take time, even if you are experienced with video production. Manim [1] is a computer graphics tool that speeds up the task of building mathematical relationships into videos (Figure 1), letting you create a graphic video image with a simple Python script.
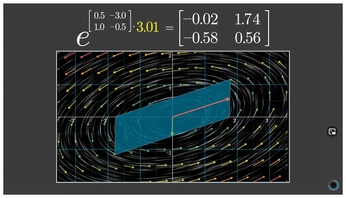
[...]
Buy this article as PDF
(incl. VAT)
Buy Linux Magazine
Subscribe to our Linux Newsletters
Find Linux and Open Source Jobs
Subscribe to our ADMIN Newsletters
Support Our Work
Linux Magazine content is made possible with support from readers like you. Please consider contributing when you’ve found an article to be beneficial.

News
-
Manjaro 26.0 Primary Desktop Environments Default to Wayland
If you want to stick with X.Org, you'll be limited to the desktop environments you can choose.
-
Mozilla Plans to AI-ify Firefox
With a new CEO in control, Mozilla is doubling down on a strategy of trust, all the while leaning into AI.
-
Gnome Says No to AI-Generated Extensions
If you're a developer wanting to create a new Gnome extension, you'd best set aside that AI code generator, because the extension team will have none of that.
-
Parrot OS Switches to KDE Plasma Desktop
Yet another distro is making the move to the KDE Plasma desktop.
-
TUXEDO Announces Gemini 17
TUXEDO Computers has released the fourth generation of its Gemini laptop with plenty of updates.
-
Two New Distros Adopt Enlightenment
MX Moksha and AV Linux 25 join ranks with Bodhi Linux and embrace the Enlightenment desktop.
-
Solus Linux 4.8 Removes Python 2
Solus Linux 4.8 has been released with the latest Linux kernel, updated desktops, and a key removal.
-
Zorin OS 18 Hits over a Million Downloads
If you doubt Linux isn't gaining popularity, you only have to look at Zorin OS's download numbers.
-
TUXEDO Computers Scraps Snapdragon X1E-Based Laptop
Due to issues with a Snapdragon CPU, TUXEDO Computers has cancelled its plans to release a laptop based on this elite hardware.
-
Debian Unleashes Debian Libre Live
Debian Libre Live keeps your machine free of proprietary software.

